Systematic Tolerance Definition
- Patrick Taliaferro
- Feb 23, 2023
- 5 min read
Updated: May 4, 2023
Written by Patrick Taliaferro, 2/20/2023
McClain Electronics Engineering, LLC
Introduction
Defining acceptable population tolerances for the electrical/mechanical/chemical parameters of a design is how one gatekeeps the quality of a serialized assembly when it arrives at the customer. These tolerances are used as conformance criteria during part testing and have real impact on non-conformance instances which result in rework (which destroys reliability) or scrap (waste); as well as having a real impact on customer satisfaction in the brand and the SIR (Service Instance Rate) metrics.
Thus, it is important to systematically set these tolerances based on real world boundaries. What follows is a system that can be used to establish tolerances.

Approach for Establishing Tolerances
The first step in establishing tolerances is to find the real-world failure criteria of a parameter or group of parameters. This is done in two ways: theoretical analysis/simulation, and real-world testing.
Theoretical analysis/simulation
The marketing and engineering roles must work together to find the best worst case scenario, wherein the system is just on the line of having a dissatisfied customer or catastrophic incident during it’s projected lifetime.
Real world testing
Testing with different bins of parts to cover the entire theoretical derived population tolerance. There are several considerations to keep in mind when determining how to test:
1.) Remember Gödel’s Incompleteness theorems, wherein it is shown that nothing may be truly proven through the use of logic or mathematics, so real world testing is necessary.
2.) The actors completing this will need to gain a randomized sample of ALL components within the sub-assembly being designed. This can be done by part binning or introducing intentional manufacturing defects to single shot parts.
3.) A representative sample size will need to be tested to verify the theoretical tolerance’s validity within the sub-assembly’s operation. This can be found using the following equation:
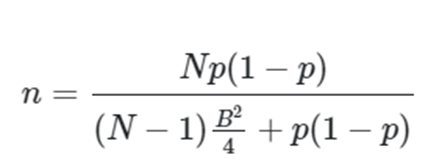
Wherein, p is a guess at the true proportion represented (things you know that you know or don’t know/total things; worst case 1/2), B is the desired bound, N is the population size, and n is the representative sample size.
4.) This can require a large amount of upfront cost which may be prohibitive for a small capital enterprise; in that case, at least sqrt(production volume/year) / 2*log(production volume/year) representative samples should be tested with parts from multiple supplier production lots.
Derating
Once the real-world failure boundary for a tolerance or group of tolerances is found, this should be de-rated by at least 10%, e.g. 3% is failure, tolerance is set to 2.7%.
Repeat
In most industries, modern iterative design practices are used, with a cycle occurring during each stage of development, allowing the final de-rated real world failure boundary to be well explored by the end of the multi-year development process. This de-rated real world failure boundary is the hard line which will be used by production staff when making quality decisions.
This implies that the sum of the error added by automatic measurement systems and the real world error of a unit’s parameters need to be enveloped within this de-rated real world failure boundary. To this end, the Supplier of a component and the Production department are usually expected to take ownership of any non-conformance, either through refunds or scrap accounts, in an effort to force them to refine their own systems to meet the necessary tolerance; with design stepping in as a support role. Any design intent/tolerance changes within the production phase of development should be met with extreme diligence and real-world testing, due to the catastrophic nature of a failure to the enterprise.
Example
Jamie works at a dishwasher manufacturer and is spec’ing out the heater which will sit within the main water pump. He is given a specific geometry, water temperature rise goal, cycle ON time, and Department of Energy enforced max power consumption.
The first step is to find the real world failure criteria, starting with theoretical failure tolerance. Based on the geometry, water temperature rise goal, and cycle ON time; Jamie derives that each unit needs a heater between 108-160W with a marginal power factor. Based on power regulations, Jamie derives that each unit needs a heater that is less then 132W nominally. This gives Jamie a theoretical heater tolerance of 108-132W, or 120W +/- 10%.
Next testing is used to validate theoretical limits with actual behavior in the system. The firm Jamie works for is targeting a yearly throughput of 160k units a year, therefore his sample size equation would be as follows. P is ½ because they are early in development and B is 0.15 because they are a commodity OEM not well known for quality and the government audits them infrequently. The following calculations determine the number of units to be tested based on population size and desired bound.


Jamie then goes to the heater supplier which they want to use and asks for a group of representative parts using material from different lot codes matching the spec’d parameters. He then has these parts installed onto 45 engineering build units randomized with other parts which are going through tolerance definition.
These 45 dishwasher units are then placed within an extended lifetime test, wherein they are repeatedly run in excess of their targeted lifetime. The power and quality of wash are monitored throughout and the results analyzed. Jamie finds that the supplier has actually manufactured a 140W nominal heater with a 0.85 power factor, leading to excessive power draw at cold start before evening out to 120W nominal. Due to this, Jamie moves the spec’d power rating to 115W +/- 10% to force the manufacturer to adjust their design so that the average power consumed is around 120W.
Jamie de-rates the power tolerance from +/- 10% to +/- 9%.
Jamie then places this nominal power rating and tolerance on the part print which will be used by the Supplier Quality and Production department as a conformance measure. Jamie will then cycle the iterative design process employed by his company, which includes 7 design iterations over a 3 year period.
After all design iterations are complete and the design is put into production, it is standard practice for Jamie’s company to force the supplier to buy back the non-conformed parts and to force the production department to eat any non-refundable part scrap. This forces any additional de-rating that has to occur to account for error introduced by manufacturing systems onto the producer of the parts and the owners of the production systems. At this stage, the designer may work with either party to refine the design but the de-rated real world failure boundary shouldn’t be expanded unless proven to be mis-set.
Conclusion
Establishing tolerances and test limits can be a difficult, but this article has laid out a systematic way to approach this complex problem. There will always be a balance between setting limits too tight and having too much fallout, and setting limits too loose and fielding products that don’t fully meet all requirements. Factors like population size and desired bound should be accounted for to establish the most robust limits that work for your application.






Comments